Мем с чуваком, открывающим дверь

Как выбрать дверь, соответствующую вашим потребностям

Первым шагом является определение целей и требований, которые вы предъявляете к двери. Определитесь с тем, что для вас главное: дизайн, безопасность, энергоэффективность или звукоизоляция.

Критерии выбора
Что нужно учесть
Дизайн
Выберите дверь, которая гармонично впишется в интерьер вашего дома

Обратите внимание на цвет, материал и стиль двери.
Безопасность
Выбирайте дверь с качественной металлической конструкцией и надежными замками. Обратитесь к специалистам, чтобы они помогли вам выбрать дверь с противовзломной системой.
Энергоэффективность
Учтите, что дверь должна быть хорошо утеплена и иметь низкий коэффициент теплопроводности

Это позволит сэкономить на отоплении и поддерживать комфортную температуру в доме.
Звукоизоляция
Если вам важна тишина внутри дома, выбирайте дверь с хорошей звукоизоляцией. Обратите внимание на толщину двери и используемые материалы.

Помимо этих критериев, учтите также размеры отверстия для двери, возможность установки дополнительных систем безопасности, таких как видеодомофон или сигнализация, а также бюджет, который вы готовы выделить на покупку двери.

Используйте представленные советы, чтобы сделать правильный выбор и найти дверь, которая лучше всего соответствует вашим потребностям.

Определение парадокса Монти Холла

Как задача парадокс Монти Холла определяется в виде описаний вышеназванной игры, наиболее распространённым среди которых является формулировка, которая была опубликована журналом «Parade Magazine» в 1990 году.

Согласно ей, человек должен представить себя участником игры, где нужно выбрать одну дверь из трёх.

За одной дверью скрывается автомобиль, а за остальными – козы. Игрок должен выбрать одну дверь, к примеру, дверь №1.

А ведущий, знающий о том, что находится за каждой дверью, открывает одну из двух дверей, которые остались, например, дверь №3, за которой стоит коза.

После этого ведущий интересуется у игрока, не желает ли он изменить свой изначальный выбор и выбрать дверь №2?

Вопрос: повысятся ли шансы игрока на выигрыш, если он изменит свой выбор?

Но после публикации этого определения выяснилось, что задача игрока сформулирована несколько неверно, т.к. не обговорены все условия.

К примеру, ведущий игры может выбрать стратегию «адского Монти», предлагая изменить выбор только в том случае, если игрок изначально угадал дверь, за которой находится автомобиль.

И становится ясно, что изменение выбора приведёт к стопроцентному проигрышу.

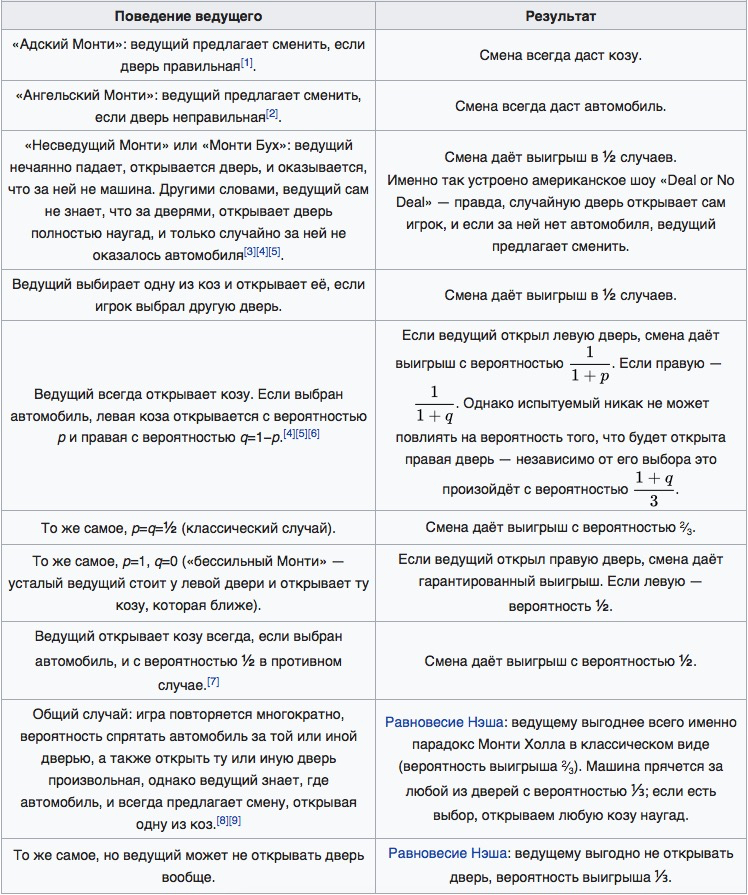
Поэтому, наибольшую популярность получила постановка задачи с особым условием №6 из специальной таблицы:

• Автомобиль может с одинаковой вероятностью находиться за каждой дверью
• Ведущий всегда обязан открывать дверь с козой, кроме той которую выбрал игрок, и предлагать игроку возможность изменения выбора
• Ведущий, имея возможность открыть одну из двух дверей, выбирает любую с одинаковой вероятностью

Представленный ниже разбор парадокса Монти Холла рассматривается именно с учётом этого условия. Итак, разбор парадокса.

Парадокс в игре телешоу «Let’s Make a Deal»

Один из парадоксов, который вызывает жаркие споры среди любителей головоломок, называется парадоксом Монти Холла. Назван он в честь ведущего телешоу в США под названием «Let’s Make a Deal». На телешоу ведущий предлагает открыть одну из трех дверей, где в качестве приза находится автомобиль, в то время когда за другими двумя находятся по одной козе.

Участник игры делает свой выбор, но ведущий, зная где находится авто, открывает при этом не ту дверь, которую указал игрок, а другую, в которой находится коза и предлагает сменить первоначальный выбор игрока. Для дальнейшего разбора мы принимаем именно этот вариант поведения ведущего, хотя на самом деле он может периодически меняться. Другие варианты сценария развития мы просто перечислим ниже в статье.

Разбор парадокса Монти Холла

Есть три варианта развития событий:

Дверь 1	Дверь 2	Дверь 3	Результат, если менять выбор	Результат, если не менять выбор
Авто	Коза	Коза	Коза	Авто
Коза	Авто	Коза	Авто	Коза
Коза	Коза	Авто	Авто	Коза

Во время решения представленной задачи обычно приводятся такие рассуждения: ведущий в каждом случае убирает одну дверь с козой, следовательно, вероятность нахождения автомобиля за одной из двух закрытых дверей приравнивается к ½, независимо от того, какой выбор был сделан изначально. Однако это не так.

Смысл в том, что, делая первый выбор, участник разделяет двери на A (выбранную), B и C (оставшиеся). Шансы (P) на то, что машина стоит за дверью A, равны 1/3, а на то, что она за дверьми B и C равны 2/3. И шансы на успех при выборе дверей B и C вычисляются так:

P(B) = 2/3 * ½ = 1/3

P(C) = 2/3 * ½ = 1/3

Где ½ является условной вероятностью того, что машина находится именно за этой дверью, при условии, что машина не за той дверью, что выбрал игрок.

Ведущий, открывая заведомо проигрышную дверь из двух оставшихся, сообщает игроку 1 бит информации и изменяет тем самым условные вероятности для дверей B и C на значения 1 и 0. Теперь шансы на успех будут вычисляться так:

P(B) = 2/3*1 = 2/3

P(C) = 2/3*0 = 0

И получается, что если игрок изменит свой изначальный выбор, то его шанс на успех будет равен 2/3.

Объясняется это следующим образом: изменяя свой выбор после манипуляций ведущего, игрок выиграет, если изначально он выбрал дверь с козой, т.к. ведущий открывает вторую дверь с козой, а игроку остаётся лишь поменять двери. Выбрать же изначально дверь с козой можно двумя способами (2/3), соответственно, если игрок заменит двери, то выиграет с вероятностью 2/3. Именно из-за противоречия такого вывода интуитивному восприятию задача и получила статус парадокса.

Интуитивное восприятие говорит о следующем: когда ведущий открывает проигрышную дверь, перед игроком встаёт новая задача, на первый взгляд не связанная с изначальным выбором, т.к. коза за открываемой ведущим дверью будет там в любом случае, независимо от того, проигрышную или выигрышную дверь изначально выбрал игрок.

После открытия ведущим двери игрок должен снова сделать выбор – либо остановиться на прежней двери, либо выбрать новую. Это значит, что игрок делает именно новый выбор, а не меняет изначальный. И математическим решением рассматриваются две последовательные и связанные друг с другом задачи ведущего.

Но нужно иметь в виду, что ведущий открывает дверь именно из тех двух, которые остались, но не ту, что выбрал игрок. А значит, шанс на то, что машина находится за оставшейся дверью, увеличиваются, т.к. ведущий её не выбрал. Если же ведущий знает, что за выбранной игроком дверью стоит коза, всё-таки её откроет, он тем самым заведомо снизит вероятность того, что игрок выберет правильную дверь, ведь вероятность успеха станет равна ½. Но это уже игра по иным правилам.

А вот ещё одно объяснение: допустим, игрок играет по представленной выше системе, т.е. из дверей B или C всегда выбирает ту, что отличается от изначального выбора. Проиграет он в том случае, если изначально выбрал дверь с автомобилем, т.к. впоследствии выберет дверь с козой. В любом другом случае игрок выиграет, если изначально выбрал проигрышный вариант. Однако вероятность того, что изначально он выберет его, равна 2/3, из чего следует, что для успеха в игре сначала нужно сделать ошибку, вероятность которой в два раза больше вероятности правильного выбора.

Третье объяснение: представим, что дверей не 3, а 1000. После того как игрок сделал выбор, ведущий убирает 998 ненужных дверей – остаются только две двери: выбранная игроком и ещё одна. Но шанс на то, что машина за каждой из дверей совсем не ½. Скорее всего (0,999%) машина будет за той дверью, которую игрок не выбрал изначально, т.е. за дверью, отобранной из оставшихся после первого выбора 999 других. Примерно так же нужно и рассуждать при выборе из трёх дверей, пусть шансы на успех и снижаются и становятся 2/3.

И последнее объяснение – замена условий. Допустим, что вместо того, чтобы делать изначальный выбор, например, двери №1, и вместо открытия двери №2 или №3 ведущим, игрок должен сделать верный выбор с первого раза, если ему известно, что вероятность успеха с дверью №1 равна 33%, но об отсутствии машины за дверьми №2 и №3 он не знает ничего. Из этого следует, что шанс на успех с последней дверью будет составлять 66%, т.е. вероятность победы увеличивается вдвое.

Но каково будет положение дел, если ведущий станет вести себя иначе?

Новые мемы со смешными ситуациями при открытии двери

Открытие двери — действие, которое мы все выполняем множество раз в течение дня. Но иногда это действие может привести к неожиданным и смешным ситуациям. Мы собрали для вас самые свежие мемы, которые появились в интернете именно на тему комичных моментов при открывании двери.

1. Мем 1: «Кот, который прячется за дверью».

   На этом меме изображен кот, который решил прячется за дверью и его маленькие лапки выглядывают снизу. Видимо, кот пытается создать иллюзию, что он нигде не причастен к происходящему, хотя все очевидно.

2. Мем 2: «Почтальон и я».

   На этом меме изображена ситуация, когда человек, открывая дверь, обнаруживает почтальона, принесшего пакеты. Но на фото отчетливо видно, что человек был совершенно не готов к такой встрече и его выражение лица говорит о его удивлении.

3. Мем 3: «Начальник за дверью».

   На этом меме изображены два человека, которые проходят рядом с дверью. Один из них внезапно осознает, что его начальник находится рядом и внимательно наблюдает за ними. Тут у него появляется момент паники и непонимания, как себя вести в такой ситуации.

4. Мем 4: «Неожиданный визит».

   На этом меме изображена ситуация, когда человек открывает дверь и обнаруживает своих друзей, которые внезапно пришли в гости. Выражение его лица говорит о его полном непонимании и поражении от такого неожиданного визита.

Эти мемы прекрасно показывают, какие смешные и неловкие ситуации могут происходить при открывании двери. Мы надеемся, что они поднимут ваше настроение и заставят вас улыбнуться. Не забудьте поделиться этими мемами со своими друзьями — ведь смех всегда объединяет людей!

Математика парадокса

Могут ли математические формулы доказать увеличение вероятности при смене выбора?
Представим цепочку событий в виде множества, разделенного на две части, первую часть примем за X – это выбор на первом этапе ячейки сейфа игроком; и второе множество Y — оставшиеся две остальных ячейки. Вероятность (В) выигрыша для ячеек 2 и 3 можно выразить с помощью формул.

В(2) = 1/2 * 2/3 = 1/3
В(3) = 1/2 * 2/3= 1/3

Где 1/2 это вероятность, с которой банкир откроет ячейку 2 и 3 при условии, если игрок изначально выбрал ячейку без слитка.
Далее условная вероятность 1/2 при открытии банкиром ячейки с монетой изменяется на 1 и 0. Тогда формулы приобретают следующий вид:

В(2) = 0 * 2/3 = 0
B(3) = 1 * 2/3 = 1

Здесь мы наглядно видим, что вероятность выбора слитка в ячейке 3 — 2/3, а это чуть более 60 процентов.
Программист самого начального уровня может без труда проверить данный парадокс, написав программу, которая считает вероятность при смене выбора или наоборот и сверить результаты.

Сырный Джерри

Джерри проглотил целый кусок сыра и принял его форму. Субъективно — один из самых смешных мемов по «Тому и Джерри», но и один из самых абстрактных. Зато и применений у него множество: можно шакалить картинку и писать вообще не связанные с ней фразы, можно шутить над перееданием или в сотый раз обыгрывать фразу: «Он съел сыр» — настоящий постмодернизм.

Кадр разошелся по сети из Tumblr еще в конце 2014 года — первая подпись к нему: «Я знаю, он съел сыр» . Взят мем из серии «Готов быть связанным» (Fit to Be Tied), вышедший в 1952 году — это между прочим 69 серия! Она рассказывает о том, как Джерри помог псу Спайку и тот в благодарность подарил мышонку колокольчик — стоит в него позвонить и Спайк придет на помощь. Пользуясь этим, Джерри делает из Тома слугу — потом все переворачивается, и не один раз. Серия знаменита эпизодом, в котором Том издевается над Спайком, сидящим на цепи — он тоже стала мемом, но не особо массовым. У Тома вообще есть свой вариант этого мема из серии «Капканы для Джерри» (Designs on Jerry) 1955 года, в которой кот придумывает идеальную мышеловку, что не нравится Джерри. В какой-то момент на Тома упал сейф и мы получили этот легендарный кадр.

История возникновения[править | править вики-текст]

В конце 1963 года в эфир вышло новое ток-шоу под названием «Let’s Make a Deal» («Давайте договоримся»). По сценарию викторины зрители из аудитории получали призы за правильные ответы, имея шанс приумножить их, делая новые ставки, но рискуя имеющимся выигрышем. Основателями шоу являлись Стефан Хатосу и Монти Холл, последний из которых стал его неизменным ведущим на многие годы.

Одним из заданий для участников стал розыгрыш Главного приза, который был расположен за одной из трех дверей. За двумя оставшимися находились поощрительные призы, в свою очередь ведущий знал порядок их расположения. Участнику необходимо было определить выигрышную дверь, поставив на кон весь свой выигрыш за шоу.

Когда угадывающий определялся с номером, ведущий открывал одну из оставшихся дверей, за которой находился поощрительный приз, и предлагал игроку поменять первоначально выбранную дверь.

Ссылки

• Интерактивный прототип: для тех, кто хочет надурить (генерация происходит после первого выбора)
• Интерактивный прототип: реальный прототип игры (генерация карточек происходит до выбора, работа прототипа прозрачна)
• Объясняющий видеоролик на сайте Smart Videos .ru

• Weisstein, Eric W.
  Парадокс Монти Холла (англ.)
  на сайте Wolfram MathWorld .
• Парадокс Монти Холла на сайте телешоу Let’s Make a deal
• Отрывок из книги С.Лукьяненко , в котором используется парадокс Монти Холла
• Ещё одно решение по Байесу Ещё одно решение по Байесу на форуме Новосибирского Государственного Университета

Мемы, где человек открывает дверь и там оказывается неожиданность

Смешные мемы, где люди открывают дверь и находят неожиданность, стали популярными в интернете. Эти мемы вызывают улыбку и являются популярным способом поделиться юмором.

1. Мемы с друзьями

Часто мемы представляют ситуации, когда человек открывает дверь и встречает своих друзей, одних или всех сразу. Они могут быть забавными и неловкими в зависимости от контекста. Например, человек может открыть дверь и обнаружить, что его друзья дали ему сюрпризную вечеринку или они просто пришли навестить его вне планов.

2. Мемы с животными

Другой популярный вариант мемов — это ситуации, когда человек открывает дверь и видит необычных гостей. Дверь может открываться на животное, которое неожиданно появляется в доме или возле дома. Например, это может быть соседский кот, незнакомая собака или даже запугивающая диковинка, такая как кенгуру или летучая мышь.

4. Мемы с комичными ситуациями

Также существуют мемы, где человек открывает дверь и оказывается в смешной или необычной ситуации. Например, дверь может открываться на уродливый предмет или аккуратное устройство, которое вызывает улыбку и недоумение. Такие мемы предназначены для вызывания смеха и непонимания.

Заключение

Мемы, где человек открывает дверь и там оказывается неожиданность, стали популярными из-за своей комичности и способности вызывать положительные эмоции у зрителей. Они стали популярными в интернете и продолжают радовать пользователей своим веселым содержанием.

Влияние мема на культуру

Мемы — это особый вид интернет-феномена, который получил широкое распространение благодаря своей способности вызывать улыбку и стать источником развлечения для миллионов людей по всему миру. Открывая дверь в мир смешных и запоминающихся картинок и фраз, мемы стали неотъемлемой частью современной интернет-культуры и оказывают значительное влияние на многие аспекты нашей жизни.

Влияние мема на поп-культуру:

• Характерные символы и фразы: Многие мемы создают собственные символы и фразы, которые быстро становятся узнаваемыми и входят в нашу повседневную жизнь. Они могут стать популярными цитатами, использоваться в различных ситуациях и даже стать основой для нового контента.
• Изменение коммуникации: Мемы часто изменяют способы коммуникации в интернете. Они создают своеобразный язык, включающий в себя различные реакции, гиперболизированные эмоции и фразы. Использование мемов в комментариях и сообщениях стало обычным, и это позволяет выразить свои мысли и эмоции с юмором.
• Имитация мемов в разных областях искусства: Мемы вдохновляют художников, музыкантов, писателей и других творческих людей. Они становятся источником вдохновения для создания новых произведений, таких как картин и музыкальные композиции, которые отражают культурные тренды и интернет-юмор.

Влияние мема на повседневную жизнь:

Влияние мема на современные тенденции:

Создание новых трендов: Мемы могут стать источником новых трендов и модных явлений

Их популярность привлекает внимание общества и стимулирует появление новых веяний в музыке, моде, искусстве и других сферах.

Политическая рефлексия: Мемы часто используются для политической рефлексии и выражения мнений. Они могут стать инструментом для критики правительства, формирования общественного мнения и мобилизации активизма.

В целом, мемы имеют значительное влияние на современную культуру. Они создают новые формы общения, внедряются в различные области искусства, изменяют наши представления о юморе и становятся отражением нашего времени и общества.

Примечания

Wikimedia Foundation
.
2010
.

Смотреть что такое «Парадокс Монти Холла» в других словарях:

В поисках автомобиля, игрок выбирает дверь 1. Тогда ведущий открывает 3 ю дверь, за которой находится коза, и предлагает игроку изменить свой выбор на дверь 2. Стоит ли ему это делать? Парадокс Монти Холла одна из известных задач теории… … Википедия

— (Парадокс галстуков) известный парадокс, похожий на задачу о двух конвертах, также демонстрирующий особенности субъективного восприятия теории вероятностей. Суть парадокса: двое мужчин дарят друг другу на Рождество галстуки, купленные их… … Википедия

Парадокс мальчика и девочки

Задачка, на первый взгляд, абсурдная, но она строго подчиняется математической формуле и имеет два варианта решения. Итак, у некого мужчины двое детей. Один из них наверняка мальчик. Какова вероятность того, что мальчиком окажется второй?

Вариант 1. Мы рассматриваем все комбинации двоих детей в семье:

• Девочка/девочка.
• Девочка/мальчик.
• Мальчик/девочка.
• Мальчик/мальчик.

Первая комбинации нам очевидно не подходит, поэтому, исходя из трех последних, мы получаем вероятность в 1/3 того, что вторым ребенком окажется маленький мужчина.

Вариант 2. Если же представить себе такой случай на практике, откинув дроби и формулы, то, исходя из того факта, что на Земле есть только два пола, вероятность того, что вторым ребенком будет мальчик, составляет 1/2.

Парадокс спящей красавицы

Этот опыт показывает нам, как лихо можно манипулировать статистикой. Итак, “спящей красавице” вкалывают снотворное и кидают монетку. Если выпадает орел, то ее будят и эксперимент прекращается. Если же выпадает решка, то ее будят, сразу делая второй укол, и она забывает о том, что просыпалась, а после этого вновь пробуждают лишь на второй день. После полного пробуждения “красавице” неизвестно, в какой день она открыла глаза, или какова вероятность того, что монета упала решкой. По первому варианту решения вероятность выпадения решки (или орла) составляет 1/2. Суть второго варианта заключается в том, что, если проводить эксперимент 1000 раз, то в случае с орлом “красавицу” будут будить 500 раз, а с редкой – 1000. Теперь уже вероятность выпадения решки составляет 2/3.

Вопросы:

1. Первая дверь зелёного цвета. Вы открываете её, за ней комната. Вы входите внутрь. Посмотрите по сторонам. Что это за комната? Опишите как она выглядит, что находится внутри. Как вы чувствуете себя, оказавшись в этой комнате? Запомните предметы, запомните свои мысли и вернитесь обратно в коридор.

2. Вторая дверь голубого цвета. Откройте ее. Оцените комнату за ней. Размеры комнаты, обстановку. Уютно ли вам здесь. Что вы чувствуете и думаете. Запомните и возвращайтесь, продолжая свой путь.

3. Третья дверь красного цвета. Входите. Что оказалось за дверью? Какая комната? Хочется ли вам остаться здесь? Какие чувства вас посещают внутри этой комнаты?

4. Последняя дверь черного цвета. Открыв ее, вы видите четвертую комнату. Зайдите в неё. Что это за место? Что вы видите. Что вы чувствуете, находясь здесь?

Теперь возвращайтесь в реальный мир и вспоминайте по порядку и подробно все увиденное вами. Описывая комнаты, обстановку и предметы интерьера, не забывайте, что главное — это ваши чувства. В какой комнате вам было удобнее всего? Какая комната вам понравилась больше? Была более уютной и красивой? А в какой, может быть, вам стало страшно и неприятно, и захотелось выйти как можно быстрее. Какая комната была светлая, а какая темная? Где царило тепло, а где беспорядок? Отметьте для себя любые важные детали. И переходите к интерпретации ответов.

Объяснение парадокса Монти Холла

Первый выбор, который вы делаете в этой игре – случайный. Вы никак не можете даже отдаленно догадываться, за какой из трех дверей спрятан приз, поэтому рандомно указываете на первую попавшуюся. Ведущий же в свою очередь знает, где что находится. У него есть дверь с призом, дверь, на которую указали вы, и третья без приза, которую он вам и открывает в качестве первой подсказки. Вторая же подсказка кроется в самом его предложении сменить выбор.

Теперь вы уже будете выбирать не наугад одну из трех, а сможете даже изменить свое решение, чтобы получить желаемый приз. Именно предложение ведущего дает человеку веру в то, что автомобиль находится действительно не за той дверью, которую он выбрал, а за другой. В этом и заключается вся суть парадокса, так как, по сути, выбирать (хоть уже из двух, а не из трех) все равно приходится наугад, но шансы на победу возрастают. Как показывает статистика, из 30-ти игроков, которые поменяли свое решение, машину выиграли 18. А это 60%. А из тех же 30-ти человек, которые решение не изменили – всего 11, то есть 36%.

Двери перед тобой: как сделать выбор незабываемым

1. Анализируй варианты.

Перед тем как сделать выбор, необходимо внимательно проанализировать все имеющиеся варианты. Рассмотри каждую дверь, представь себя за каждой из них и задай себе вопрос – что я могу получить, открыв эту дверь? Учти все плюсы и минусы каждого варианта, чтобы принять обдуманное решение.

2. Доверься интуиции.

Иногда чувство и интуиция помогают нам принять правильное решение. Если у тебя есть ощущение, что одна из дверей – это твой путь, доверься своему внутреннему голосу. Интуиция часто оказывается верной.

3. Сделай необратимый выбор.

Чтобы сделать выбор незабываемым, нужно выбрать дверь и полностью открыть её. Не оставляй дверь приоткрытой на случай, если что-то пойдет не так. Прими свое решение и двигайся вперед с уверенностью.

Важно помнить, что сделанный выбор – это шанс, который либо красиво расцветет, либо станет уроком на опыте. Иногда неудачи приводят нас к большему счастью

Поэтому, открывая дверь, гармонизируй в себе силу принятия риска и терпение для приема окрестностей.

Иногда путь, который кажется непривлекательным, оказывается идеальным выбором. Не бойся взять на себя риск и идти в незнакомое, потому что именно там могут быть наилучшие призы.

Польский Джерри

Косолапый Джерри с крайне странным, маниакальным выражением лица. Один из древнейших мемов по «Тому и Джерри» — сегодня встречается редко, но до конца не забылся. Всегда сопровождается максимально чернушной шуткой о том, как ты делаешь что-нибудь чересчур маргинальное.

История у мема долгая. Он возник еще в 2015 году в аргентинской соцсети Taringa! с шуткой в стиле: «Когда обдолбался». Потом мем ходил в испаноязычном пространстве как реакция на все дикое с простой подписью: «Че за херня». И только в 2016-м его занесло в англоязычный интернет, откуда он перебрался и к нам. Причем попал он туда с польского сайта с подписью: «Когда смотришь документалку о холокосте в школе и тут учитель спрашивает, почему ты мастурбируешь». Потому и «польский» Джерри. Это далеко не самый мерзкий пример шуток вокруг проклятой картинки: как известно, при всей своей видимой безобидности мемы используют в самом неожиданном и жутком контексте — как это в свое время случилось с лягушонком Пепе, которого сделали символом ультраправых в США (хотя автор мема, разумеется, был не восторге).

«Польский» Джерри так разошелся, что с ним даже начали выпускать игрушки

Кадры для мема взяты из серии «Молочный путь» (The Milky Waif) 1946 года. В ней Джерри пытается выкрасть молоко у Тома, чтобы накормить подкидыша Нибблза. Ставший мемом момент настолько всрат потому, что это промежуточный кадр — Джерри на нем просто поворачивается. Нибблз, к слову, настолько раздражающий тип, что после этой серии даже лютые фанаты Джерри должны были понять страдания Тома.

Интерпретация:

1. В психологии зеленый цвет символизирует детство. Войдя в комнату за зеленой дверью — вы оказались в своем детстве. Что вы чувствовали при этом? Если вам было приятно и уютно, то значит и ваше детство было для вас приятным и светлым временем. Если вам хотелось надолго остаться в этой комнате, то, скорее всего, вы нередко в мыслях возвращаетесь в свое детство и, возможно, вам не хватает во взрослой жизни того теплого и душевного времени, заботы и участия со стороны других людей. Любые негативные мысли и чувства, возникшие в этой комнате, свидетельствуют о нерешенных детских проблемах, которые оказывают влияние на всю вашу дальнейшую жизнь. В норме, комната должна оказаться милой и уютной, но не должна вызывать особого желания в ней остаться, потому что любопытство побывать за другими дверями, должно оказаться сильнее.

2. Вторая комната за дверью голубого цвета символизирует ваше душевное состояние в настоящий момент, в эту самую минуту, когда вы проходите данный тест. Ваши ощущения расскажут о том, как вы чувствуете себя сейчас. Удобно или неудобно в этой комнате. Устраивает вас ваша настоящая жизненная ситуация или у вас присутствует желание изменить ее. В комнате был порядок или беспорядок — характеризует вас, как собранного, организованного человека или, наоборот, хаотичного и импульсивного. Комната пустая или наполнена самыми различными предметами? И т.д.

3. Третья дверь красного цвета и находящаяся за ней комната символизирует чувственную любовь и ваше отношении к ней. Большая просторная комната — вы склонны испытывать сильные чувства. Маленькое помещение — вы скованный, робкий в проявлении чувств, человек. Светлая — ваши любовные переживания лёгкие, воздушные, романтические. Тёмная — любовные чувства заставляют вас испытывать страдания. Уютная или неуютная — расскажет о том, комфортно ли вам в любви или, может быть, вы недавно пережили в любви разочарование. Яркие или тусклые цвета в комнате. Какие предметы: повседневные, обычные или эксклюзивные произведения искусства.

4. Черная дверь и комната за ней символизирует ваше отношение к профессиональной деятельности, к работе и делам. Что это была за комната? Был там порядок и лежало все на своих местах или комната была захламлена различными ненужными вещами? Хорошо ли вы ориентировались в этой комнате или совершенно растерялись? Просторная или маленькая — расскажет о возможностях применения ваших профессиональных знаний и
умений. Если вам было комфортно в этой комнате — значит и в профессиональной жизни, вы чувствуете себя безопасно и, похоже, находитесь на своем месте.

Трактовка в цифрах

Теперь дадим парадоксу Монти Холла более точное определение. Первый выбор игрока разбивает двери на две группы. Вероятность того, что приз расположен за дверью, которую вы выбрали, составляет 1/3, а за теми дверьми, что остались 2/3. Ведущий далее открывает одну из дверей второй группы. Таким образом он переносит всю оставшуюся вероятность, 2/3, на одну дверь, которую вы не выбрали и которую он не открывал. Логично, что после таких расчетов выгоднее будет сменить свое решение

Но при этом важно помнить, что шанс проиграть все-таки имеется. Порой ведущие лукавят, так как вы изначально можете ткнуть на правильную, призовую дверь, а после от нее добровольно отказаться

Все мы привыкли к тому, что математика, как точная наука, идет рука об руку со здравым смыслом. Тут дело делают цифры, а не слова, точные формулы, а не туманные размышления, координаты, а не относительные данные. Но ее новый раздел под названием теория вероятностей взорвал весь привычный шаблон. Задачи из этой области, как нам кажется, не вкладываются в рамки здравого смысла и полностью противоречат всем формулам и вычислениям. Предлагаем ниже ознакомиться с другими парадоксами теории вероятности, которые имеют нечто общее с тем, который был описан выше.

Что если увеличить количество ячеек?

Что если увеличить количество ячеек? Допустим вместо трех их будет 50. Золотой слиток будет лежать лишь только в одной ячейке, а в остальных 49 — монеты. Соответственно в отличии от классического случая вероятность попадания с ходу в цель 1/50 или 2% вместо 1/3, в то время как вероятность выбора ячейки с монетой составляет 98%. Далее ситуация развивается, как и в прежнем случае. Банкир предлагает открыть любую из 50 ячеек, участник выбирает. Допустим, игрок открывает ячейку под порядковым номеров 49. Банкир в свою очередь, как и в классическом варианте, не спешит выполнять желание игрока и открывает другие 48 ячеек с монетами и предлагает поменять свой выбор на оставшуюся под номером 50.

Здесь важно понимать, что банкир открывает именно 48 ячеек, а не 30, и оставляет при этом 2, включая выбранную игроком. Именно такой выбор позволяет парадоксу идти в разрез с интуицией

Как и в случае с классическим вариантом, открытие банкиром 48 ячеек оставляет только один единственный альтернативный вариант для выбора. Случай варианта меньшего открытия ячеек не позволяет поставить в один ряд задачу с классикой и ощутить парадокс.

Но раз уж мы и коснулись такого варианта, то давайте предположим, что банкир оставляет не одну, кроме выбранной игроком, а несколько ячеек. Представлено, как и прежде, 50 ячеек. Банкир после выбора игрока открывает только одну ячейку, оставляя при этом закрытыми 48 ячеек, включая выбранную игроком. Вероятность выбора слитка с первого раза 1/50. В сумме вероятность нахождения слитка в остальных ячейках 49/50, которая в свою очередь раскидывается не на 49, а на 48 ячеек. Не сложно посчитать, что вероятность нахождения слитка в таком варианте равна (49/50)/48=49/2900 . Вероятность пусть не на много, но все равно выше, чем 1/50 приблизительно на 1%.

Как мы и упоминали в самом начале ведущий Монти Холл в классическом сценарии игры с дверьми, козами и призовым авто может изменять условия игры и вместе с нем и вероятность выигрыша.

Примечания

1. Selvin, Steve. A problem in probability (letter to the editor) (англ.) // American Statistician  (англ.) (рус. : journal. — Vol. 29, no. 1. — P. 67. — JSTOR .
2. Selvin, Steve. On the Monty Hall problem (letter to the editor) (англ.) // American Statistician  (англ.) (рус. : journal. — Vol. 29, no. 3. — P. 134. — JSTOR .
3. ↑
4. Granberg, Donald (1996). «To Switch or Not to Switch». Appendix to vos Savant, Marilyn, The Power of Logical Thinking. St. Martin’s Press. ISBN 0-312-30463-3, ( в «Книгах Google»).
5. Granberg, Donald and Brown, Thad A. (1995). «The Monty Hall Dilemma, » Personality and Social Psychology Bulletin 21(7): 711—729.
6. ↑
7. ↑ Rosenthal, Jeffrey S. (2005b): Struck by Lightning: the Curious World of Probabilities. Harper Collings 2005, ISBN 978-0-00-200791-7.